所谓时空数据,顾名思义,包含了两个维度的信息:空间信息与时间信息。空间信息,以地理位置点最为基础,还包括线、多边形以及更为复杂的多维结构。最典型的时空数据,莫过于移动对象的轨迹点数据,如每隔5秒钟记录的车辆实时位置信息。这类数据,在物联网领域司空见惯,在可预见的未来,这类数据将会出现爆炸性的增长。
用HBase存放时空数据
时空数据,尤其是移动对象位置点数据,结构简单,但关于吞吐量的要求却往往很高。单从这点信息来看,这类数据属于HBase的适用范畴。
先不谈论时间纬度与复杂的多边形数据,我们先从最简单的地理位置点数据开始,探讨一下如果用HBase来存储这类数据会遭遇哪些技术挑战。
地理位置点Point中包含两个信息:经度X与纬度Y,按照传统的思路,将一个Point存成一行数据,而经度X与纬度Y则分别是构成这行数据的两个列,可以为每一个Point设置一个ID,并以此ID作为数据RowKey。所有的Points在表中按ID字典顺序存放。
围绕地理位置点的典型的查询方式,如“查询某一个建筑附近有哪些酒店?”,按照刚刚表设计思路,数据如按主键ID顺序存放,某个建筑附近的所有酒店,它们在主键顺序上却未必是相邻的,因此,这个查询可能涉及扫描大量的无关数据。
可见,针对最简单的时空数据类型,传统HBase表设计思路已经显得非常低效,传统关系型数据库基于B-Tree的数据组织结构也更是疲于应对。再放大到整个时空数据的范畴,要支持的典型场景更为复杂:
- 查询某一个地理区域在某个历史时间范围内发生的关键事件
- 查询某一个地理区域的人流量、车流量信息
- 查询某一天上午先后在A,B,C三个地理区域出现过的具有某些特征的人
- 查询某嫌疑人在某一天的行动轨迹
归根结底,HBase中的数据按照RowKey单维度排序组织,而我们现在却面临的是一个多维数据问题。因此,HBase如果想很好的支持时空数据的存储,需要引入时空索引技术。
从上面的查询场景来看,原生HBase的访问接口难以直接支持这些能力,因此,时空数据领域需要更加专业的访问接口,这是GeoMesa项目存在的关键原因。
常见的时空索引技术
关于时空索引,已经有不少常见的技术,这里,我们主要介绍一下R-Trees、Quad-Trees、K-D Trees以及Space Filling Curve这四种技术。
R-Trees
R-Trees源自论文《R-Trees: A Dynamic Index Structure For Spatial Searching》,下面的图也源自此论文:
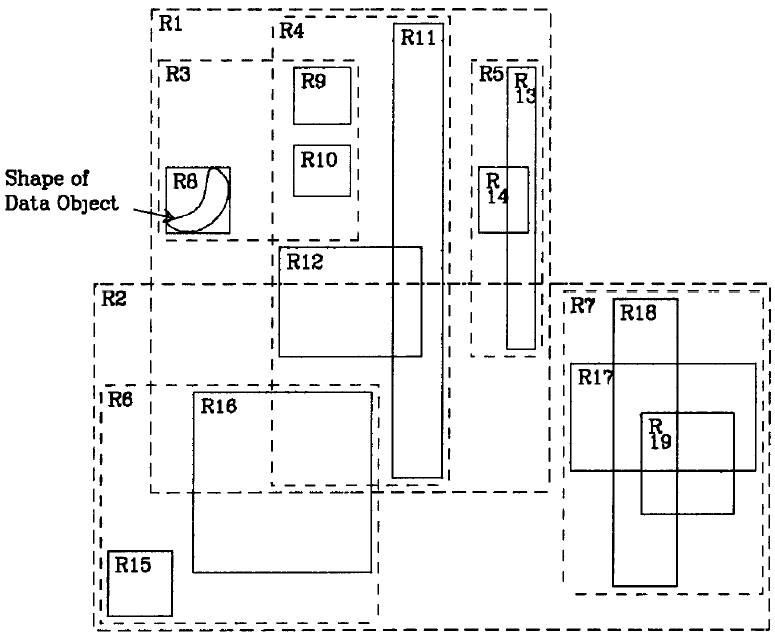
R-Trees基于这样的思想设计:
每一个空间对象,如一个多边形区域,都存在一个最小的矩形,能够恰好包含此时空对象,如上图中的矩形R6所包含的弯月形区域。这个最小包围矩形被称之为MBR(Minimum Bounding Rectangle)。
多个相邻的矩形,可以被包含在一个更大的最小包围矩形中。如R6、R9以及R10三个矩形,可以被包含在R3中,而R11与R12则被包含在R4中。
继续迭代,总能找到若干个最大的区域,以一种树状的形式,将所有的时空对象给容纳进去,如上图中的R1, R2。这样,整个树状结构,呈现如下:
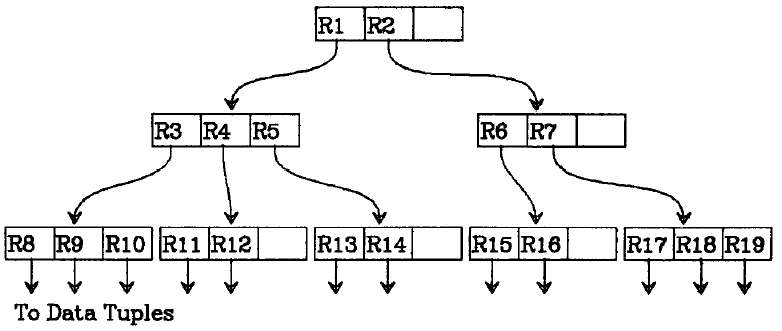
从最小的矩形区域,到最大的矩形区域,就好比地图中的行政区域划分:村 -> 县 -> 市 -> 省份。查询时,先从锁定的最大区域开始,逐级缩小比例尺后,就可找到最终的对象。如若将上图中的R1与R2理解成两个平级的”行政区域”,却又存在本质的区别:不同的行政区域,并不存在相互重叠,而R1与R2却可能是重叠的。
R-Trees的定义:
\1. 每一个Leaf Node包含m到M个索引记录(Root节点除外)。
\2. 每一个索引记录是一个关于(I, tuple-identifier)的二元组信息,I是空间对象的最小包围矩形,而tuple-identifier用来描述空间对象本身。
\3. 每一个Non-leaf节点,包含m到M个子节点(Root节点除外)。
\4. Non-leaf节点上的每一个数据元素,是一个(I, child-pointer)的二元组信息,child-pointer指向其中一个子节点,而I则是这个子节点上所有矩形的最小包围矩形。
如上图中,R3、R4以及R5,共同构成一个non-leaf节点,R3指向包含元素R8,R9以及R10的子节点,这个指针就是child-pointer,而与R8,R9以及R10相关的最小包围矩形,就是I。
\5. Root节点至少包含两个子节点,除非它本身也是一个Leaf Node。
\6. 所有的Leaf Nodes都出现在树的同一层上。
从定义上来看,R-Trees与B-Trees存在诸多类似:Root节点与Non-Leaf节点,均包含限定数量的子节点;所有的Leaf Nodes都出现在树的同一层上。这两种树也都是自平衡的。
前面也已经提到了,B-Trees主要用来存放一维排序的数据元素,而R-Tree存放的则是多维空间数据元素。从查询方式上来看,两者也存在显著的差异:B-Trees更擅长于数据点查,它的设计并不利于数据的范围查询。基于空间元素的查询,却以范围查询为主,而且往往需要对多个子树进行并行查询,例如,在地图上划定某一个区域,查询这个区域内有哪些公园,可能有多个子树都与划定的这个区域存在交集。从这一点看来,R-Tree的搜索性能其实并没有很好的保障。
R-Trees有多种变种,如R+-Trees,R*-Trees,X-Trees, M-Trees,BR-Trees等等,不再展开过多的介绍。
Quad-Trees
同很多数据结构类似,Quad-Trees也存在多种变种,最初的Quad-Trees设计源自论文《Quad Trees: A Data Structure for Retrieval on Composite Keys》,下图源自论文,是关于Quad-Trees的直观呈现:
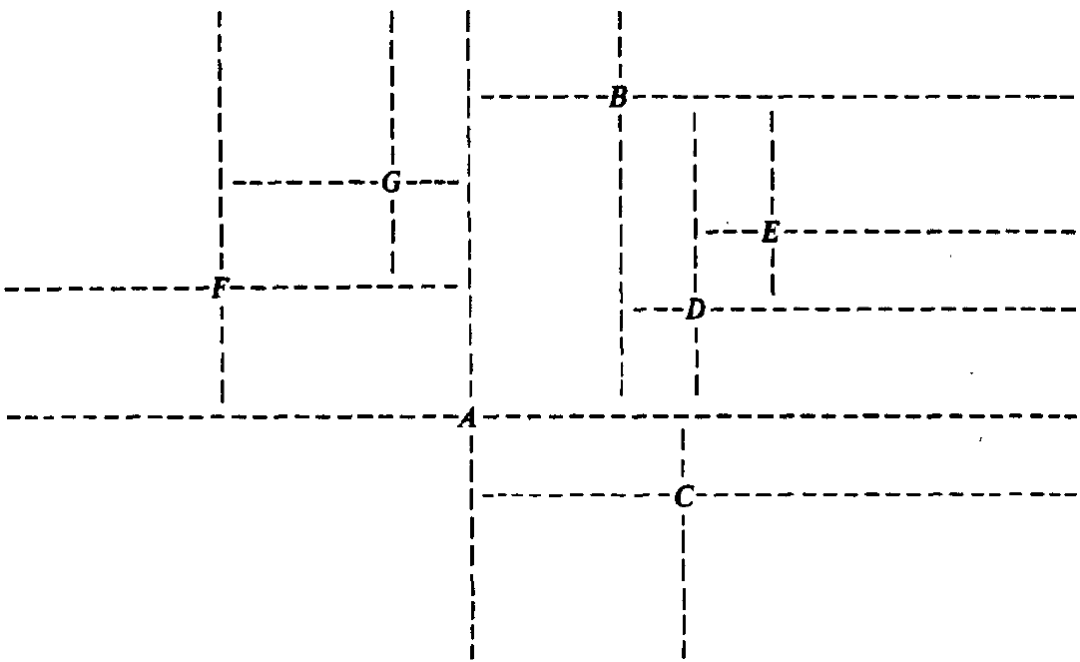
上图中的A,B,C,E,F,G均为Point,以每一个Point作为中心点,可以将一个区间分成4个象限。
假设,先写入Point A,以A为中心,将整个区间分成了4个象限。
写入Point B,Point B位于A的东北象限中,同样,以B为中心,依然可以将A东北象限进一步细分为4个子象限。
写入Point C,Point C位于A的东南象限中,以C为中心,可以将A的东南象限细分成4个子象限。
…..
任何新写入的一个Point,总能找到一个某一个已存在的Point的子象限,来存放这个新的Point。
整个树状结构呈现如下:
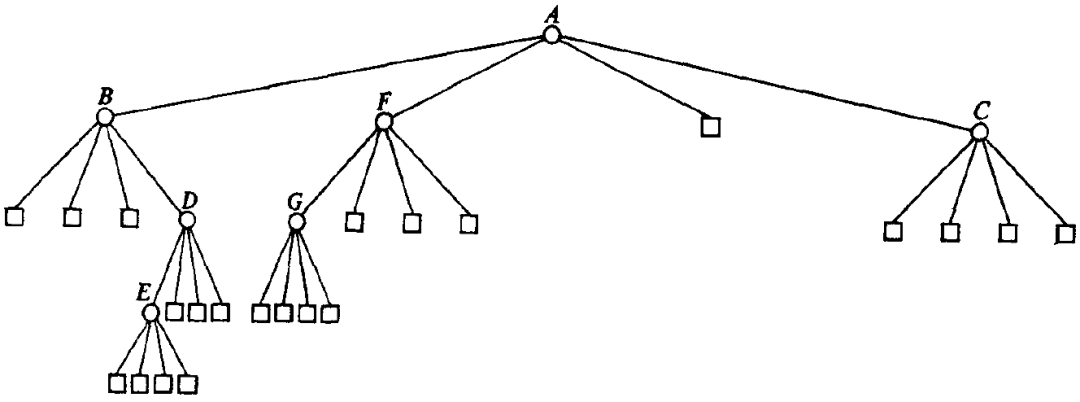
可见,Quad-Trees有几个鲜明的特点:1. 对于非叶子节点,均包含4个子节点,对应4个面积不一的象限。2.不平衡,树的结构与数据的写入顺序直接相关。3.有空的Leave Nodes,且所有的Leave Nodes则是”参差不齐”的(并不一定都出现在树的同一层中)。4.数据既可能出现在分枝节点中,也可能出现在叶子节点中。
因为Quad-Trees存在诸多变种,为了有所区分,上面提到的最简单的这种Quad-Tree,被称之为Point Quad-Trees。还有一种典型的Quad-Trees,被称之为Point Region QuadTrees(简称为PR QuadTrees):
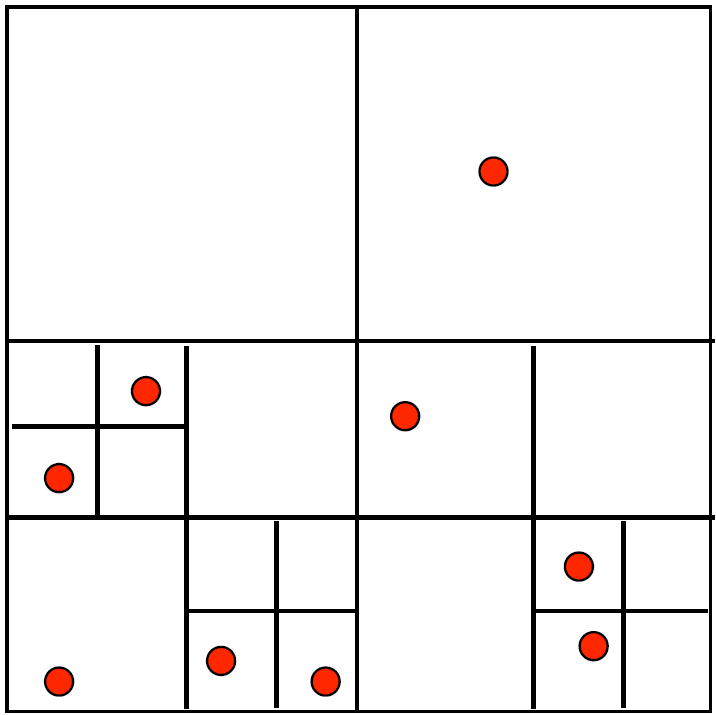
PR Quad-Trees中,每一次迭代出来的4个象限,面积相同,且不依赖于用户数据Point作为分割点,或者说,数据分区与用户数据无关。每一个划分出来的子象限中,只允许存在一个Point。
与Point Quad-Trees相比,PR Quad-Trees允许两份不同的数据集,拥有相同的分区信息。但PR Quad-Trees存在的问题也明显:1. 两个相邻的Points,可能在树的Level高度上相隔甚远。2.两份数据集如果追求相同的分区信息,可能需要进行足够粒度的分割,这可能导致空间浪费。
K-D Trees
K-D Trees是一种针对高维点向量数据的索引结构,一棵简单的K-D Tree如下图所示(原图源自James Fogarty的”K-D Trees and Quad Trees”,但为了更直观,关于分区分割线的线条做了改动):
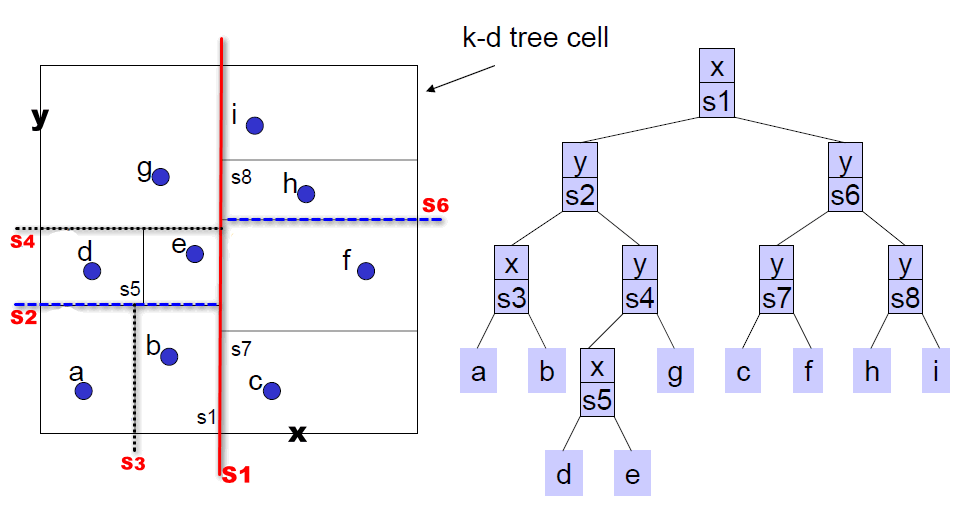
与Quad Trees思想类似,K-D Trees也是将整个区间进行不断分割,不同之处在于,Quad Trees每一次迭代,将一个区间分割成四个象限,而K-D Trees则是分成左右或上下两个区间。如上图所示:S1把整个空间分成了左右两个区间,左侧区间中,又被S2横向分割成了上下两个区间,而S3又在S2的分割基础上,将下部分分割成了左右两个区间,….
如果已经存在一批Points,则较容易针对这批数据构建出一棵趋于平衡的K-D Tree,如若接收实时写入的数据,或者说数据更新频繁,K-D Tree则难以维持平衡态,除非对整棵树进行重构。
Space Filling Curve
如果将一个完整的二维空间,分割成一个个大小相同的矩形,可以将Space Filling Curve简单理解为它是一种将所有的矩形区域用一条线”串”起来的方法,因”串”的方式不同,也就引申出了不同的Space Filling Curve算法。
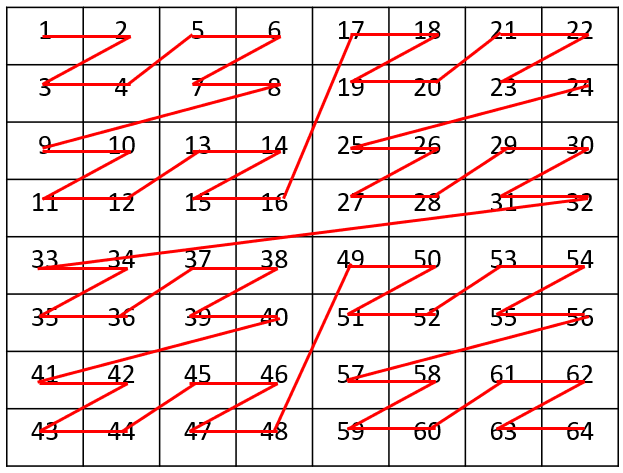
比较典型的如Z-Order Curve:
再如Hilbert Curve:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-43z6zHOE-1620871556108)(data:image/gif;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQImWNgYGBgAAAABQABh6FO1AAAAABJRU5ErkJggg==)]
Space Filling Curve事实上是为空间数据提供了一种一维排序的方法,它拉近了空间数据与传统数据库的距离:因为这意味着可以使用传统的B-Tree或B+-Tree索引,来存储空间数据。
我们再借助于Z-Order的迭代构建过程,来加深读者关于Space Filling Curve的理解:
如果将整个区间划分成4个象限,第一轮迭代就是将这4个象限利用Z-Order曲线连接起来:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zTNW3nCz-1620871556108)(data:image/gif;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQImWNgYGBgAAAABQABh6FO1AAAAABJRU5ErkJggg==)]
而后,将第一轮迭代中的每一个象限,再进一步细分成4个象限,这样共变成了16个区间。在第二轮迭代中,再将16一个小区间用Z-Order曲线连接起来:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zlvUOgjf-1620871556110)(data:image/gif;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQImWNgYGBgAAAABQABh6FO1AAAAABJRU5ErkJggg==)]
第三轮迭代再进一步拆分、连接,变成下图的样子:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DbbDkGxl-1620871556111)(data:image/gif;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQImWNgYGBgAAAABQABh6FO1AAAAABJRU5ErkJggg==)]
每一次迭代,都是在上一次迭代的”方格”基础上,将每一个”方格”拆成了4个”子方格”,这种思想与Quad-Tree的思路是一致的,尤其是PR Quad-Tree,因此,也可将Space Filling Curve理解成一种高效构建Quad-Tree的方式,但需要说明的一点是,Z-Order论文的发布时间要远早于Quad-Tree论文的时间。
GeoHash
GeoHash可以将Point编码成一个字符串,如:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vke3Ejyf-1620871556112)(data:image/gif;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQImWNgYGBgAAAABQABh6FO1AAAAABJRU5ErkJggg==)]
http://geohash.org这个网站提供了经纬度与Geohash的在线转换能力。从编码结果来看,可以发现三个特点:
越高的精度,字符串越长,可对比上表中的P1到P3的Geohash值变化。
P3所表示的区域涵盖了P2,而P2涵盖了P1,这层关系,在生成的Geohash值中这样体现:
“ws10rn6y”(对应P2)以”ws10rn”(对应P3)为前缀
“ws10rn6yp9ms”(对应P1)以”ws10rn6y”(对应P2)为前缀。
位置相近的点,生成的Geohash值也相似,如P2与P4,两者纬度相同,经度仅差0.001,在生成的Geohash值中仅最后一个字符有区别。
GeoMesa官方资料中,也给出了这样一个典型的例子:
针对 (-78.48, 38.03),编码的过程,如下:
第1步:经度二分
规则:先将完整的坐标系统(-180.000 -90.000, 180.000 90.000)按经度中点0.000进行二分,如果处于左边则编码为0,处于右边,则编码为1。
结果:因 (-78.48, 38.03)处于左侧区间(-180.000, 0.000),因此,实际编码为0。此时, (-78.48, 38.03)所处的区间被缩小为(-180.000 -90.000, 0.000 90.000)。
第2步:纬度二分
规则:基于第1步的结果,再将(-180.000 -90.000, 0.000 90.000)按纬度中点0.000进行二分,如果处于上侧则编码为1,处于下侧,则编码为0。
结果:因 (-78.48, 38.03)处于上侧区间(-180.000, 0.000),编码为1,与第一步的结果结合在一起,编码变为”01″。此时, (-78.48, 38.03)所处的区间被缩小为(-180.000 0.000, 0.000 90.000)。
第3步:经度二分
规则:基于第2步的结果,再将(-180.000 0.000, 0.000 90.000)按经度中点-90.000进行二分,同样,如果处于左侧则编码为0,处于右侧,则编码为1。
结果:因 (-78.48, 38.03)处于上侧区间(-90.000, 0.000),编码为1,与前两步的结果结合在一起,编码变为”011″。此时, (-78.48, 38.03)所处的区间被缩小为(-90.000 0.000, 0.000 90.000)。
第4步:纬度二分
…..
就这样,经度纬度不断交替二分迭代,每一步的输出结果如下表所示:
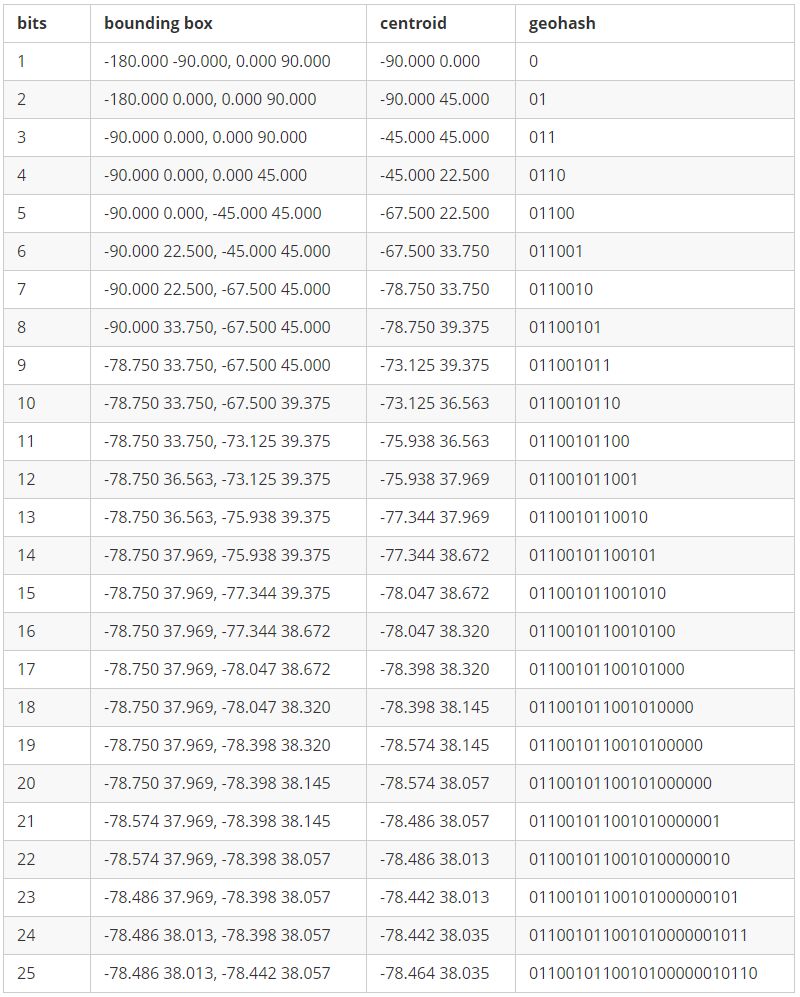
关于上表中的Bounding Boxes的不断编码,可直观的体现在下图中:
通过Base-32 Encoding,可以将上表中的编码结果进一步编码成字符串。例如,基于Base-32编码规则:
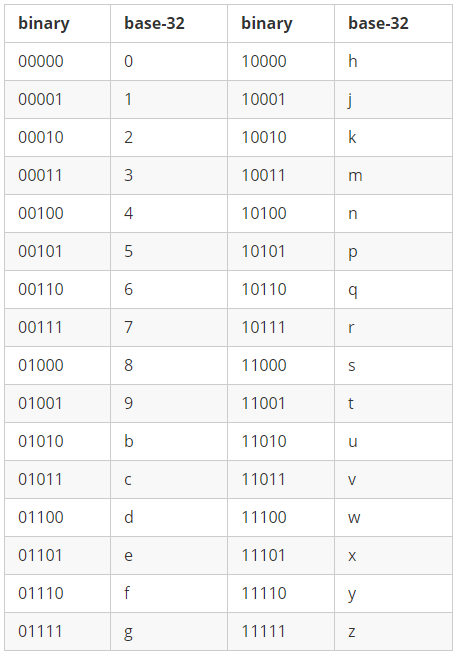
因此,(-78.48, 38.03)的编码为01100 10110 01010 00000 10110,将其转换成对应的字符:
01100 -> d
10110 -> q
01010 -> b
00000 -> 0
10110 -> q
连在一起,(-78.48, 38.03)的最终编码结果变为:dqb0q
经Geohash编码后,其顺序与Z-Order编码保持一致,因此,也可以将Geohash是针对Z-Order算法的一种编码机制。Geohash编码带来的显著优势是:以字符串字典顺序表达Z-Order顺序,利用字符串的前缀匹配规则,也可快速实现多边形区域的重叠计算,但在编码效率上却并无任何优势,如sfcurve项目中提供的Z2编码算法,性能要远高于Geohash算法。
哪种时空索引可应用于HBase?
HBase基于LSM-Tree架构,底层HFile文件以B+ Tree形式组织。在不影响HBase现有架构的基础上,我们来分别探讨一下各种时空索引与HBase结合的可能性。
从R-Trees的原始论文描述来看,它的设计是为了充分利用Disk Page的优势,这一点与B-Tree类似。它支持良好的数据随机写入能力,能够自平衡,从设计上来看,非常适合于矩形/多边形空间对象的存储。既然是致力于磁盘上的索引设计,对HBase现有架构带来较大的侵入性,即使能对HBase进行改造,与B-Tree类似的这种设计,已经被证明难以支撑高吞吐量数据写入。如果不做任何改造,我们只能考虑如何将R-Trees的数据映射到HBase的KeyValue模型中:HBase的数据按RowKey排序,从而能够按照RowKey快速检索,如果将R-Trees的数据以HBase原生数据形态组织,自然希望能提供一种方法,使得R-Trees中的数据排序方式与RowKey的排序一致,或者说,如何为R-Trees中的数据对象找到一种RowKey生成机制,使得R-Trees中的数据顺序就是RowKey的字典顺序。但我们知道,R-Trees中,其实已经弱化了数据对象”排序”的含义,一个节点与子节点之间,更多是一种包含于被包含的关系,一个空间对象可能归属于不同的分枝,这取决于那种划分方案更优,当一个Leaf Node承载的对象过多时,也可能出现Split。如果按照传统的树遍历的顺序来理解R-Trees中的对象排序,这种排序是不确定的。这意味着,我们无法构建出一种确定顺序的RowKey。
再来看一下K-D Trees:K-D Trees是针对高维点向量而设计,用来存储二维的Point数据,自然也能很好的应对。K-D Trees的结构,与数据的写入顺序强相关,也可以说,同样的一批数据,因顺序不同,所构成的树的结构截然不同,这个问题也存在于Point Quad Trees中,因树结构的不确定性,它们与HBase结合的最大障碍,依然在于如何将Trees中的数据映射到KeyValue模型中。
PR Quad Tree的分区则不依赖于数据本身,更与数据的写入顺序无关,但PR Quad Tree限制每一个Point都独占一个小方格的设计,使得每一个Point可能处在树的不同层次/高度中,而且随着数据的不断写入,同一个Point所处的高度可能会发生变化:如原来某一个方格中只有一个Point,但如果有新的数据写入后,这个方格需要进一步被分拆成4个新的子方格,原来的Point在树中的位置也发生了变化,因此,PR Quad Tree也无法直接应用于HBase。
如果对PR Quad Tree进行稍加改造:
- 将完整空间经过X次迭代后,预先将其划分成4^x个小方格。
- 所有的Point都必须存放在最小的方格中。
- 不限制每一个小方格中存放的Points的数量。
这样,带来了三点”确定性”:树的层次是确定的,每一个小方格在树中的访问路径是确定的,每一个Point所属的小方格也是确定的。因此,只要我们存在一种方法,将每一个小方格的访问路径,映射成HBase的RowKey,就完美解决了时空Points数据存放在HBase中的问题,这种思路正是Spatial Filling Curve的核心思想。
我们提到了两种常见的Spatial Filling Curve: Z-Order Curve与Hilbert Curve。评价一种Spatial Filling Curve的优劣,有两个关键的维度:
- 距离保留度:将二维空间对象映射成一维曲线后,两个对象在二维区间上如果是相近的,那么,在一维曲线中也应当是相近的。一个更优的曲线,理应更大程度上在一维曲线中维持对象在二维空间上的距离,或者说,应该有更高的距离保留度。对于查询而言,更高的距离保留度,也往往意味着更高的Caching命中率。
- 编码复杂度:可以简单理解为将二维空间对象映射成一维曲线的计算复杂度。
Z-Order曲线在距离保留度上,略弱于Hilbert曲线,但在编码复杂度上,却比Hilbert曲线更低,这是GeoMesa选择Z-Order曲线的关键原因。
